Neue Formeln und Messunsicherheit
Christopher • 14. März 2022
Neue Formeln
und
Messunsicherheit
Neue Formeln
- Zweck von Experimenten
- Experimentelle Bestimmung neuer Formeln
Messunsicherheit
- Umgang mit Messwerten
- Bestimmung von Messunsicherheiten
- Relative Fehler
Theoretiker
und
Experimentatoren
Theoretiker
- Wie könnte die Welt sein?
Experimentatoren
- Welche mögliche Welt ist unsere
- Können Theorie nie belegen
Beispiel (nicht für ABI)
- Maxwell-Gleichungen: Licht feste Geschwindigkeit
- Newton: keine absolute Ruhe
$\rightarrow$ Geschwindigkeit relativ - Spezielle Relativitätstheorie: Raum und Zeit relativ
- Michelson-Morley Experiment: Lichtgeschwindigkeit konstant
Was ist ein Experiment?
- Reproduzierbare Situation
- Störenden Variablen ausgeschaltet\kompensiert
- Jeweils eine unabhängige Variable verändert
- Beobachtung aller abhängigen Variablen
Unbekannte Situation experimentell erfassen
"Machen Sie Messungen! Von Anfang an mit theoretischen Modellen zu arbeiten ist Alchemie."
—Unbekannter Professor
Stromwaage
- Stromstärke $I$
- Leiterlänge $l$
- Kraft auf Leiter $F_L$
- Temperatur
- Windgeschwindigkeit
- Mondphase
Stromwaage
Unabhängige Variablen
- Stromstärke $I$
- Leiterlänge $l$
Abhängige Variablen
- Kraft auf Leiter $F_L$
Veränderung der Stromstärke
\[\begin{aligned}
l = 8cm
\end{aligned}\]
| $I$ in $A$ | $5,0$ | $10,0$ | $15,0$ |
|---|---|---|---|
| $F_L$ in $mN$ | $1,9$ | $3,8$ | $5,8$ |
| $\frac{F_L}{I}$ in $\frac{mN}{A}$ | $0,38$ | $0,38$ | $0,39$ |
\[\begin{aligned}
F_L \sim I \text{, wenn } l = \text{konst}
\end{aligned}\]
Veränderung der Leiterlänge
\[\begin{aligned}
I = 10A
\end{aligned}\]
| $l$ in $cm$ | $1,0$ | $2,0$ | $4,0$ | $8,0$ |
|---|---|---|---|---|
| $F_L$ in $mN$ | $0,4$ | $0,9$ | $2,0$ | $3,8$ |
| $\frac{F_L}{l}$ in $\frac{mN}{cm}$ | $0,40$ | $0,45$ | $0,50$ | $0,48$ |
\[\begin{aligned}
F_L \sim l \text{, wenn } I = \text{konst}
\end{aligned}\]
Stromwaage
\[\begin{aligned}
F_L &\sim I \text{, wenn } l = \text{konst} \\
F_L &\sim l \text{, wenn } I = \text{konst}
\end{aligned}\]
\[\begin{aligned}
F_L &\sim I \cdot l \\
F_L &= B \cdot I \cdot l
\end{aligned}\]
$\Rightarrow$ neue Grösse $B$, abhängig vom Magnetfeld
Unterschied: Anzahl signifikanter Stellen
Signifikante Stellen
$4562,30m$
Signifikante Stellen
- $\htmlClass{sig}{4562,3\underline{0}}m$
- $0000\htmlClass{sig}{4562,3\underline{0}}m$
- $\htmlClass{sig}{4562,3\underline{0}}\htmlClass{wrong}{0000}$
- $0,00\htmlClass{sig}{45623\underline{0}}\vphantom{}\cdot 10^6m$
- $\htmlClass{sig}{4,5623\underline{0}}\vphantom{}\cdot 10^3m$
- $\htmlClass{sig}{4,5623\underline{0}}km$
- Von erster nicht-Null Stelle zur Rundungsstelle
- Führende Nullen irrelevant
- Folgende Nullen täuschen falsche
Genauigkeit
vor
$\rightarrow$ Rundungsstelle ist letzte Stelle! - Zehnerpotenz kann angepasst werden (zwischen $0,1$ und $1000$ gut)
Signifikante Stellen—Zweck
- Impliziert Messunsicherheit
- $0,0\htmlClass{sig}{69\underline{0}}m$ $\Rightarrow 0,0\htmlClass{sig}{69\underline{0}}m \pm 0,0000\htmlClass{sig}{50}m$
- $0,0\htmlClass{sig}{69\underline{0}}\htmlClass{wrong}{000}m$ $\Rightarrow 0,0\htmlClass{sig}{69\underline{0}}\htmlClass{wrong}{000}m \pm 0,0000\htmlClass{wrong}{000}\htmlClass{sig}{50}m$
- Messunsicherheit explizit mit zwei signifikanten Stellen anzugeben
Sonderfälle
- Natürliche Zahlen \[\begin{aligned} k &= 2 \end{aligned}\]
- Exakt bekannte, unendlicher Menge Nachkommastellen \[\begin{aligned} \frac{1}{7} &= 0,1429\dots \end{aligned}\]
- Exakt bekannte, endlicher Menge Nachkommastellen \[\begin{aligned} h &= 6,62607015 \cdot 10^{-34} Js \\ &= 6,6261\dots\vphantom{} \cdot 10^{-34} Js \end{aligned}\]
Wie soll ich denn jetzt runden?
"Ich runde grundsätzlich auf volle Tausender."
—Frau Struthoff
Wie soll ich denn jetzt runden?
- Im TI gar nicht!
- Endergebnisse, um keine zu hohe Genauigkeit vorzutäuschen
-
Faustregel für's ABI:
Anzahl signifikanter Stellen der ungenausten Messgrösse + 1
Beispiel
\[\begin{aligned} F_L &= \htmlClass{sig}{17,\underline{1}}mN \\ I &= \htmlClass{sig}{5,6\underline{4}}A \\ l &= \htmlClass{sig}{4,\underline{0}}cm \\ B &= \frac{F_L}{I \cdot l} = \frac{\htmlClass{sig}{17,\underline{1}}mN} {\htmlClass{sig}{5,6\underline{4}}A \cdot \htmlClass{sig}{4,\underline{0}}cm} \\ &= 0,07579\dots T \\ &\approx \htmlClass{fragment}{\htmlClass{sig}{75,\underline{8}}mT} \end{aligned}\]Ablesen aus Graphiken
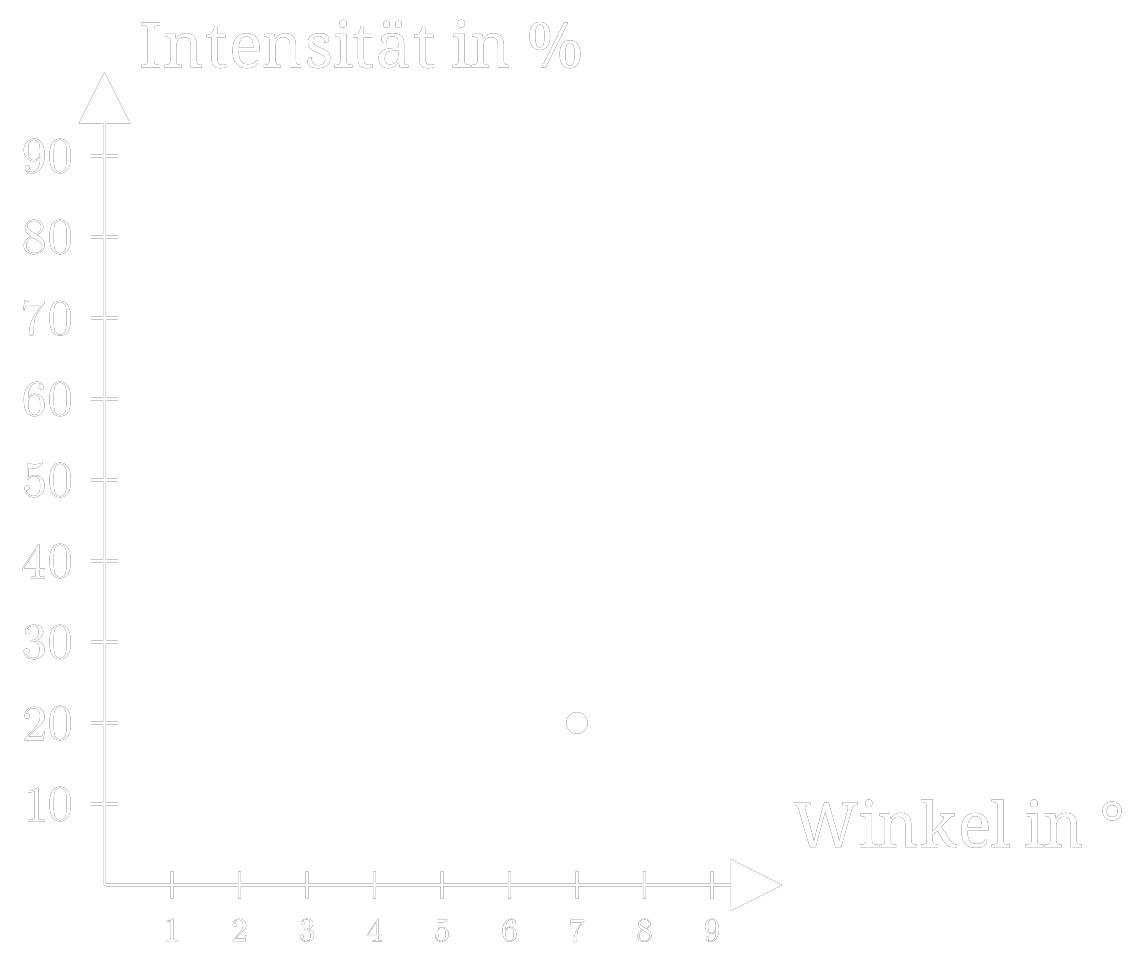
- Ableseungenauigkeit mit signifikanten Stellen kennzeichnen
- Faustregel: $\pm$ viertel Skaleneinheit
- Einteilung von $1\degree$
$\rightarrow$ Unsicherheit von
$\pm \frac{1}{4}\degree = \pm 0,25\degree$ - z.B. $\htmlClass{sig}{\underline{7}}\degree$,
da $0,5\degree > 0,25\degree > 0,05\degree$
Bestimmung der Messunsicherheit
"Ermitteln Sie [...] die absolute Messunsicherheit der kurzwelligen Grenze des Wellenlängenbereichs." —Abituraufgabe 2021 II
- Fehlerfortpflanzungsrechnung
- Minimal-Maximal-Abschätzung
Minimal-Maximal-Abschätzung
\[\begin{aligned}
\lambda_{max} &= \frac{1}{500}mm \cdot \sin\left( \arctan\left( \frac{5,1cm}{19,8cm} \right)
\right) &= 500nm \\
\lambda_{min} &= \frac{1}{500}mm \cdot \sin\left( \arctan\left( \frac{4,9cm}{20,4cm} \right)
\right) &= 470nm
\end{aligned}\]
\[\begin{aligned}
d_k &= 5,0cm &\pm 0,1cm \\
a &= 20,1cm &\pm 0,3cm
\end{aligned}\]
Absolute Messunsicherheit:
\[\begin{aligned} \frac{|500nm - 470nm|}{2} \Rightarrow \pm \htmlClass{sig}{15}nm \end{aligned}\]
\[\begin{aligned} \frac{|500nm - 470nm|}{2} \Rightarrow \pm \htmlClass{sig}{15}nm \end{aligned}\]
Minimal-Maximal-Abschätzung
\[\begin{aligned}
\lambda = \frac{1}{500}mm \cdot \sin\left( \arctan\left( \frac{5,0cm}{20,1cm} \right)
\right) = 498nm
\end{aligned}\]
Relative Messunsicherheit:
\[\begin{aligned}
\frac{|500nm - 470nm|}{498nm} = \htmlClass{sig}{6,0}\%
\end{aligned}\]
Absolute Messunsicherheit:
\[\begin{aligned} \frac{|500nm - 470nm|}{2} \Rightarrow \pm \htmlClass{sig}{15}nm \end{aligned}\]
\[\begin{aligned} \frac{|500nm - 470nm|}{2} \Rightarrow \pm \htmlClass{sig}{15}nm \end{aligned}\]
Relative Fehler
\[\begin{aligned}
\frac{|\text{Gemessener Wert} - \text{Literaturwert}|}{\text{Literaturwert}} =
\frac{\text{Differenz}}{\text{Literaturwert}} \\
\end{aligned}\]
\[\begin{aligned}
\frac{|5 \cdot 10^{-34}Js - 6,62607015 \cdot 10^{-34}Js|}
{6,62607015 \cdot 10^{-34}Js} = \htmlClass{sig}{25}\%
\end{aligned}\]
Massnahmen zur Messunsicherheitsverringerung
- Genauere Messgeräte
- Grössere Längen
- Mehrfache Längen (vom linken 3. Maximum zum rechten 3. statt 1. zum 0.)
- Mehrere Messungen (andere Varianten und Bildung des Mittelwerts)
- Bessere Isolierung gegen / Kompensierung von Umwelteinflüssen (Temperatur, Erschütterungen)
Neue Formeln—Zusammenfassend
- Abhängige, unabhängige Variablen identifizieren
- pro Versuch eine unabhängige Variable variieren
- funktionale Zusammenhänge aufstellen
Messunsicherheit—Zusammenfassend
- Im TI nicht runden
- Nicht nach Rundungsstelle angeben
- Eine signifikante Stelle mehr als ungenauste Messgrösse
- Ablesen aus Graphik: $\pm$ viertel Skaleneinheit
- Minimal-Maximal-Abschätzung für explizite Messunsicherheit (zwei signifikante Stelle angeben)
- Relative Fehler: $\frac{\text{Differenz}}{\text{Literaturwert}}$
Quellen
- Niedersachsen KC
- Wikipedia/Signifikante Stellen
- Lernhelfer/Fehlerbetrachtung
- Leifiphysik/Stromwaage
- Leitfaden Naturwissenschaft—Michael Klotsche
- A Brief History of Time—Stephen Hawking
The End
Neue Formeln und Messunsicherheit